The DDPM Model

Notes on the DDPM diffusion generative model.

Introduction

This post covers the denoising diffusion probabilistic model as introduced in the paper “Denoising Diffusion Probabilistic Models” by Ho et al. . Diffusion models were first introduced in “Deep Unsupervised Learning using Nonequilibrium Thermodynamics” by Sohl-Dickstein et al. , but gained popularity after the DDPM paper demonstrated that diffusion models could generate high-quality images.

Familiarity with generative models, particularly the variational autoencoder model, is assumed. A good resource on VAEs is Variational Autoencoders, by Brian Keng . I will not cover improvements to the basic DDPM model, guidance, score-based generative models, or applications here, although I hope to cover them in future posts.

I am heavily indebted to Understanding Diffusion Models: A Unified Perspective by Calvin Luo for the presentation of the DDPM math and The Annotated Diffusion Model by Niels Rogge and Kashif Rasul for learning about how to implement a DDPM. Be sure to check out those posts!

The presentation of the math follows the overall structure of Understanding Diffusion Models: A Unified Perspective; I have tried to present my own take on the derivations. The code snippets are based on the code from The Annotated Diffusion Model , which is based on the PyTorch implementation by Phil Wang , which in turn is based on the original Tensorflow implementation by the DDPM authors . An accompanying code repo can be found here.

If you aren’t interested in the nitty gritty of diffusion model math, you can skip down to the “Summary of DDPM Math” section, which contains a self-contained summary of the important equations for understanding and implementing a DDPM model.

Hierarchical Variational Autoencoders

In a standard variational autoencoder (VAE) model, we have a set of data variables $x$ and latent variables $z$, and we are interested in modeling the marginal distribution of the data $p(x)$. This is done through learning an encoder $q_\phi(z \mid x)$ which is a variational approximation to the true posterior $p(z \mid x)$ and a decoder $p_\theta(x \mid z)$ which recovers the data distribution conditioned on the latent variables $z$. This model is typically trained by maximizing a variational lower bound (VLB) or evidence lower bound (ELBO) :

\[\begin{equation} \label{eq:vae_elbo} \log{p(x)} \geq \mathbb{E}_{z \sim q_\phi(z | x)}[\log{p_\theta(x | z)}] - D_{KL}(q_\phi(z | x) || p(z)) \end{equation}\]

A hierarchical variational autoencoder (HVAE) extends this model by introducing higher level latents $z_1, z_2, \ldots, z_T$, where a higher level latent variable $z_t$ is allowed to condition on all lower level latents $z_1, \ldots, z_{t - 1}$. As with a VAE, maximizing the log likelihood $\log{\int{p(x, z_{1:T})dz_{1:T}}}$ of this model is generally intractable, but we can still derive an ELBO using a variational approximation $q_\phi(z_{1:T} \mid x)$:

\[\begin{equation} \label{eq:hvae_elbo} \begin{split} \log{p(x)} & = \log{\int{p(x, z_{1:T})dz_{1:T}}} \\ & = \log{\int{\frac{p(x, z_{1:T})q_\phi(z_{1:T} | x)}{q_\phi(z_{1:T} | x)}dz_{1:T}}} \\ & = \log{\mathbb{E}_{z_{1:T} \sim q_\phi(z_{1:T} | x)}[\frac{p(x, z_{1:T})}{q_\phi(z_{1:T} | x)}]} \\ & \geq \mathbb{E}_{z_{1:T} \sim q_\phi(z_{1:T} | x)}[\log{\frac{p(x, z_{1:T})}{q_\phi(z_{1:T} | x)}}] \end{split} \end{equation}\]

The last line follows by Jensen’s inequality for a concave function $f$: $f(\mathbb{E}[x]) \geq \mathbb{E}[f(x)]$.

To simplify $(\ref{eq:hvae_elbo})$ further, we need an expression for the joint distribution $p(x, z_{1:T})$ and the posterior $q_\phi(z_{1:T} \mid x)$.

Markovian Hierarchical Variational Autoencoders

We will now make the following simplifying assumption: the latent variables $z$ satisfy the Markov property as we move from higher-level latents to lower level latents. That is, we can express the decoding transition from $z_{t+1}$ to $z_t$ as $p(z_t \mid z_{t + 1})$. The generative process (starting from $z_T$, whose prior distribution $p(z_T)$ we specify by construction) is then a Markov chain, and we call a HVAE satisfying this property a Markovian hierarchical variational autoencoder (MHVAE). This has a nice visual representation as follows:

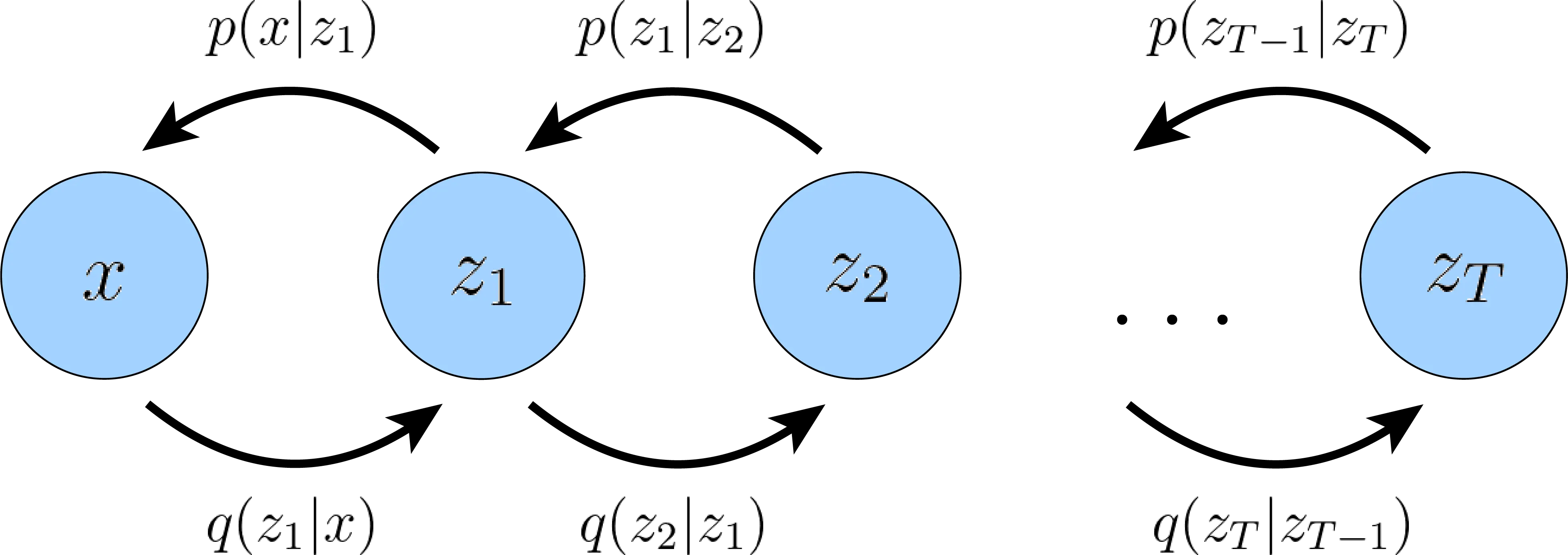
A visual representation of a MHVAE model. Image from Understanding Diffusion Models: A Unified Perspective.

Using the Markov property, we can write down the joint distribution of a MHVAE explicitly as

$\begin{equation} \label{eq:mhvae_joint_dist} p_\theta(x, z_{1:T}) = p_\theta(x | z_1)\prod_{t = 2}^{T}{p_\theta(z_{t - 1} | z_t)} \cdot p(z_T) \end{equation}$ Similarly, we can write the posterior distribution of the latent variables as

$\begin{equation} \label{eq:mhvae_post} q_\phi(z_{1:T} | x) = q_\phi(z_1 | x)\prod_{t = 2}^{T}{q_\phi(z_t | z_{t - 1})} \end{equation}$ To make the math simpler, we will make the following assumption:

Diffusion Model Latent Dimension Assumption. The dimension of the latent variables $z_{1:T}$ equals the dimension of the data variable $x$.

We will thus rename the data variable to $x_0$ and the latent variables to $x_{1:T}$. With our new notation, we can rewrite the joint distribution as follows

$\begin{equation} \label{eq:reverse_diff_process} p_\theta(x_{0:T}) = p(x_T)\prod_{t = 1}^{T}{p_\theta(x_{t - 1} | x_t)} \end{equation}$ This Markov chain defines the reverse diffusion process, starting from the prior $p(x_T)$. Similarly, for the posterior, we have

$\begin{equation} \label{eq:forward_diff_process} q_\phi(x_{1:T} | x_0) = \prod_{t = 1}^{T}{q_\phi(x_t | x_{t - 1})} \end{equation}$ This is also a Markov chain and defines the forward diffusion process. We will see how to interpret these terms later.

Deriving an ELBO

Now we can simplify our ELBO further:

\[\begin{equation} \label{eq:mhvae_elbo1_deriv} \begin{split} \log{p(x)} & \geq \mathbb{E}_{x_{1:T} \sim q_\phi(x_{1:T} | x_0)}[\log\frac{p_\theta(x_{0:T})}{q_\phi(x_{1:T} | x_0)}] \\ & = \mathbb{E}_{x_{1:T} \sim q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)\prod_{t = 1}^{T}{p_\theta(x_{t - 1} | x_t)}}{\prod_{t = 1}^{T}{q_\phi(x_t | x_{t - 1})}}] \\ & = \mathbb{E}_{x_{1:T} \sim q_\phi(x_{1:T} | x_0)}[\log\frac{p_\theta(x_0 | x_1)\prod_{t = 2}^{T}{p_\theta(x_{t - 1} | x_t)} \cdot p(x_T)}{\prod_{t = 1}^{T - 1}{q_\phi(x_t |x_{t - 1})} \cdot q_\phi(x_T | x_{T - 1})}] \\ & = \mathbb{E}_{x_{1:T} \sim q_\phi(x_{1:T} | x_0)}[\log\frac{p_\theta(x_0 | x_1)\prod_{t = 1}^{T - 1}{p_\theta(x_{t} | x_{t + 1})} \cdot p(x_T)}{\prod_{t = 1}^{T - 1}{q_\phi(x_t |x_{t - 1})} \cdot q_\phi(x_T | x_{T - 1})}] \\ & = \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log{p_\theta(x_0 | x_1)}] + \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)}{q_\phi(x_T | x_{T - 1})}] \\ & + \sum_{t = 1}^{T - 1}{\mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p_\theta(x_t | x_{t + 1})}{q_\phi(x_t | x_{t - 1})}]} \\ & = \mathbb{E}_{q_\phi(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] + \mathbb{E}_{q_\phi(x_{T - 1}, x_T | x_0)}[\log\frac{p(x_T)}{q_\phi(x_T | x_{T - 1})}] \\ & + \sum_{t = 1}^{T - 1}{\mathbb{E}_{q_\phi(x_{t - 1}, x_t, x_{t + 1} | x_0)}[\log\frac{p_\theta(x_t | x_{t + 1})}{q_\phi(x_t | x_{t - 1})}]} \\ & = \mathbb{E}_{q_\phi(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] - \mathbb{E}_{q_\phi(x_{T - 1}, x_T | x_0)}[\log\frac{q_\phi(x_T | x_{T - 1})}{p(x_T)}] \\ & - \sum_{t = 1}^{T - 1}{\mathbb{E}_{q_\phi(x_{t - 1}, x_t, x_{t + 1} | x_0)}[\log\frac{q_\phi(x_t | x_{t - 1})}{p_\theta(x_t | x_{t + 1})}]} \\ \end{split} \end{equation}\]

Since $q_\phi(x_{t - 1}, x_t, x_{t + 1} \mid x_0) = q_\phi(x_t \mid x_{t -1}, x_{t + 1}, x_0)q_\phi(x_{t - 1}, x_{t + 1} \mid x_0)$ by the chain rule, which we can simplify to $q_\phi(x_t \mid x_{t - 1})q_\phi(x_{t - 1}, x_{t + 1} \mid x_0)$ using the Markov property, we can rewrite the terms in the sum as a KL divergence:

\[\begin{equation} \label{eq:mhvae_elbo_1_kl_div_ex} \begin{split} L_t & = \mathbb{E}_{q_\phi(x_{t - 1}, x_t, x_{t + 1})}[\log{\frac{q_\phi(x_t | x_{t - 1})}{p_\theta(x_t | x_{t + 1})}}] \\ & = \mathbb{E}_{q_\phi(x_{t - 1}, x_{t + 1})}[D_{KL}(q_\phi(x_t | x_{t - 1}) || p_\theta(x_t | x_{t + 1}))] \\ \end{split} \end{equation}\]

Similarly $q_\phi(x_{T - 1}, x_T \mid x_0) = q_\phi(x_{T - 1} \mid x_0)q_\phi(x_T \mid x_{T - 1})$, so we can rewrite the second and third terms as expectations over KL divergences as follows:

\[\begin{equation} \label{eq:vdm_elbo1} \begin{split} \log{p(x_0)} \geq & \mathbb{E}_{q_\phi(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] \\ & - \sum_{t=1}^{T-1}{\mathbb{E}_{q_\phi(x_{t-1}, x_{t+1} | x_0)}[D_{KL}(q_\phi(x_t | x_{t-1}) || p_\theta(x_t | x_{t+1}))]} \\ & - \mathbb{E}_{q_\phi(x_{T-1} | x_0)}[D_{KL}(q_\phi(x_T | x_{T-1}) || p(x_T))] \end{split} \end{equation}\]

Thus, the ELBO can be written as a sum of terms $L_0 + L_1 + \ldots + L_t + \ldots + L_T$ which can be interpreted as follows:

Reconstruction term $L_0 = \mathbb{E}_{q_\phi(x_1 \mid x_0)}[\log{p_\theta(x_0 \mid x_1)}]$: this term expresses how well we are able to recover the original data $x$ from the first level latent $x_1$, and is the direct analogue of the reconstruction term in the VAE ELBO.
Consistency terms $L_t = \mathbb{E}_{q_\phi(x_{t-1}, x_{t+1} \mid x_0)}[D_{KL}(q_\phi(z_t \mid z_{t-1}) \vert\vert p_\theta(z_t \mid z_{t+1}))]$: these terms capture how close the noising transition from $x_{t - 1}$ to $x_t$ matches the denoising transition from $x_{t + 1}$ to $x_t$. Ideally, we want these to have the same distribution: we should end up with data at the same noise level whether we are going forwards or backwards.
Prior Matching term $L_T = \mathbb{E}_{q_\phi(x_{T - 1} \mid x_0)}[D_{KL}(q_\phi(x_T \mid x_{T-1}) \vert\vert p(x_T))]$: this captures how well our last forward transition $q_\phi(x_T \mid x_{T - 1})$ matches the latent prior $p(x_T)$, and is the direct analogue of the prior matching term in the VAE ELBO.

The ELBO we derived also has a nice visual representation:

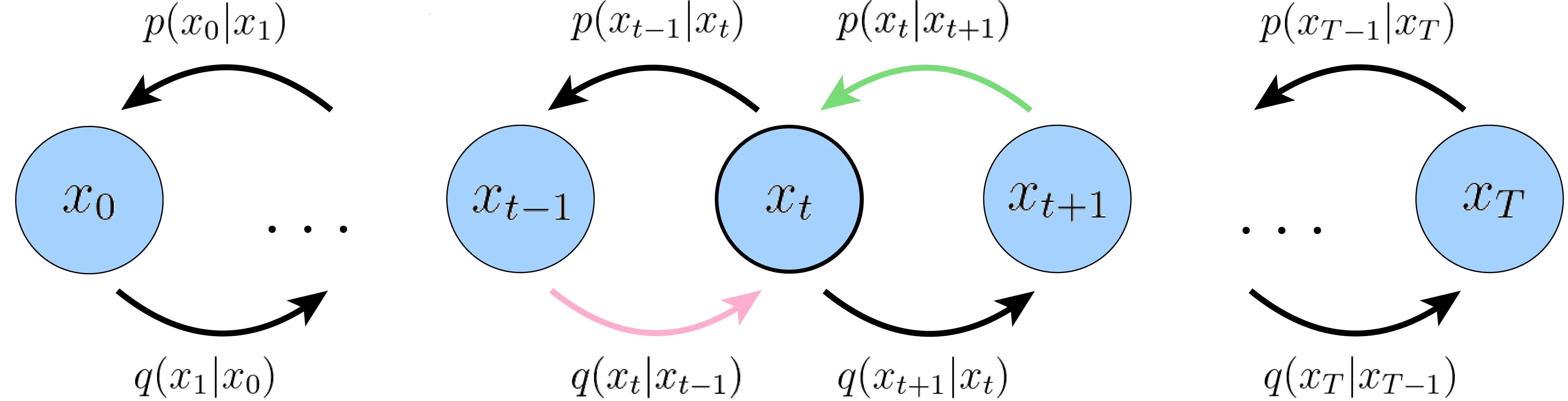
Each consistency term of the variational lower bound compares the KL divergence of the forward noising transition (pink arrow) and reverse denoising transition (green arrow); to maximize the VLB, we want to make these distributions as similar as possible. Image from Understanding Diffusion Models: A Unified Perspective.

We could try to directly optimize this ELBO, but because the consistency terms $L_{1:T - 1}$ are expectations over two random variables $x_{t-1}$ and $x_{t+1}$, we would need to take a large number of samples to reduce their variance to an acceptable level.

Deriving a Lower Variance ELBO

Let us try to rewrite the ELBO such that all of our expectations are over only one random variable. We can begin the derivation as follows:

$\begin{equation} \label{eq:vdm_elbo2_deriv1} \begin{split} \log{p(x)} & \geq \mathbb{E}_{x_{1:T} \sim q(x_{1:T} | x_0)}[\log\frac{p_\theta(x_{0:T})}{q_\phi(x_{1:T} | x_0)}] \\ & = \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)\prod_{t = 1}^{T}{p_\theta(x_{t-1} | x_t)}}{\prod_{t = 1}^{T}{q_\phi(x_t | x_{t-1})}}] \\ & = \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)p_\theta(x_0 | x_1)\prod_{t = 2}^{T}{p_\theta(x_{t-1} | x_t)}}{q_\phi(x_1 | x_0)\prod_{t = 2}^{T}{q_\phi(x_t | x_{t-1})}}] \end{split} \end{equation}$ Here we can make a key insight: due to the Markov property, we can write

$\begin{equation} \label{eq:vdm_elbo2_key} q_\phi(x_t | x_{t-1}) = q_\phi(x_t | x_{t-1}, x_0) = \frac{q_\phi(x_{t-1} | x_t, x_0)q_\phi(x_t | x_0)}{q_\phi(x_{t-1} | x_0)} \end{equation}$ Plugging this in to the product in the denominator of $(\ref{eq:vdm_elbo2_deriv1})$, we get:

$\begin{equation} \label{eq:vdm_elbo2_deriv2} \begin{split} \log{p(x)} & \geq \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)p_\theta(x_0 | x_1)\prod_{t = 2}^{T}{p_\theta(x_{t-1} | x_t)}}{q_\phi(x_1 | x_0)\prod_{t = 2}^{T}{q_\phi(x_t | x_{t-1})}}] \\ & = \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)p_\theta(x_0 | x_1)\prod_{t = 2}^{T}{p_\theta(x_{t-1} | x_t)}}{q_\phi(x_1 | x_0)\prod_{t = 2}^{T}{\frac{q_\phi(x_{t-1} | x_t, x_0)q_\phi(x_t | x_0)}{q_\phi(x_{t-1} | x_0)}}}] \\ \end{split} \end{equation}$ The $\frac{q_\phi(x_t \mid x_0)}{q_\phi(x_{t-1} \mid x_0)}$ terms in the denominator product conveniently telescope to $\frac{q_\phi(x_T \mid x_0)}{q_\phi(x_1 \mid x_0)}$, which leaves us with the following:

\(\begin{equation} \label{eq:vdm_elbo2_deriv3} \begin{split} \log{p(x)} & \geq \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)p_\theta(x_0 | x_1)\prod_{t = 2}^{T}{p_\theta(x_{t-1} | x_t)}}{q_\phi(x_1 | x_0)\prod_{t = 2}^{T}{\frac{q_\phi(x_{t-1} | x_t, x_0)q_\phi(x_t | x_0)}{q_\phi(x_{t-1} | x_0)}}}] \\ & = \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)p_\theta(x_0 | x_1)\prod_{t = 2}^{T}{p_\theta(x_{t-1} | x_t)}}{q_\phi(x_T | x_0)\prod_{t = 2}^{T}{q_\phi(x_t | x_{t-1})}}] \\ & = \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log{p_\theta(x_0 | x_1)}] + \mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p(x_T)}{q_\phi(x_T | x_0)}] \\ & + \sum_{t=2}^{T}{\mathbb{E}_{q_\phi(x_{1:T} | x_0)}[\log\frac{p_\theta(x_{t-1} | x_t)}{q_\phi(x_{t-1} | x_t, x_0)}]} \\ & = \mathbb{E}_{q_\phi(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] + \mathbb{E}_{q_\phi(x_T | x_0)}[\log\frac{p(x_T)}{q_\phi(x_T | x_0)}] \\ & + \sum_{t=2}^{T}{\mathbb{E}_{q_\phi(x_{t-1}, x_t | x_0)}[\log\frac{p_\theta(x_{t-1} | x_t)}{q_\phi(x_{t-1} | x_t, x_0)}]} \\ & = \mathbb{E}_{q_\phi(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] - \mathbb{E}_{q_\phi(x_T | x_0)}[\log\frac{q_\phi(x_T | x_0)}{p(x_T)}] \\ & - \sum_{t=2}^{T}{\mathbb{E}_{q_\phi(x_{t-1}, x_t | x_0)}[\log\frac{q_\phi(x_{t-1} | x_t, x_0)}{p_\theta(x_{t-1} | x_t)}]} \\ \end{split} \end{equation}\) We can immediately convert the second term $\mathbb{E}_{q_\phi(x_T \mid x_0)}[\log\frac{q_\phi(x_T \mid x_0)}{p(x_T)}]$ into a KL divergence $D_{KL}(q_\phi(x_T \mid x_0) \vert\vert p(x_T))$. For the terms in the third term sum, we can rewrite $q_\phi(x_{t - 1}, x_t \mid x_0)$ as $q_\phi(x_{t - 1} \mid x_t, x_0)q_\phi(x_t \mid x_0)$ using the chain rule of probability, so we can also turn these terms into a KL divergence inside an expectation over $x_t \sim q(x_t \mid x_0)$: $\mathbb{E}_{q_\phi(x_t \mid x_0)}[D_{KL}(q_\phi(x_{t-1} \mid x_t, x_0) \vert\vert p_\theta(x_{t-1} \mid x_t))]$. Thus we get the following ELBO:

$\begin{equation} \label{eq:vdm_elbo2} \begin{split} \log{p(x)} \geq & \mathbb{E}_{q_\phi(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] \\ & - \sum_{t=2}^{T}{\mathbb{E}_{q_\phi(x_{t}| x_0)}[D_{KL}(q_\phi(x_{t-1} | x_t, x_0) || p_\theta(x_{t-1} | x_t))]} \\ & - D_{KL}(q_\phi(x_T | x_0) || p(x_T)) \\ \end{split} \end{equation}$ As with the first ELBO $(\ref{eq:vdm_elbo1})$ we derived, we can write the ELBO as a sum of terms $L_0 + L_1 + \ldots + L_{t - 1} + \ldots + L_T$:

Reconstruction term $L_0 = \mathbb{E}_{q_\phi(x_1 \mid x_0)}[\log{p_\theta(x_0 \mid x_1)}]$: this term remains unchanged from $(\ref{eq:vdm_elbo1})$, and captures how well we can reconstruct the original data $x_0$ from the first latent variable $x_1$.
Denoising matching terms $L_{t - 1} = \mathbb{E}_{q_\phi(x_t \mid x_0)}[D_{KL}(q_\phi(x_{t-1} \mid x_t, x_0) \vert\vert p_\theta(x_{t-1} \mid x_t))]$: these terms capture how close the denoising transition $p_\theta(x_{t-1} \mid x_t)$ matches the “ground truth” denoising transition $q_\phi(x_{t-1} \mid x_t, x_0)$. Since we have access to the original data $x_0$, we can tractably recover $x_{t - 1}$ in the ground truth denoising transition (also called the “forward process posterior”).
Prior matching term $L_T = D_{KL}(q_\phi(x_T \mid x_0) \vert\vert p(x_T))$: this expresses how well our forward sampling process $q(x_T \mid x_0)$ matches the latent prior $p(x_T)$, and is an analogue of the prior matching term in the VAE ELBO and our previous ELBO $(\ref{eq:vdm_elbo1})$.

Similarly, we can visualize this ELBO:

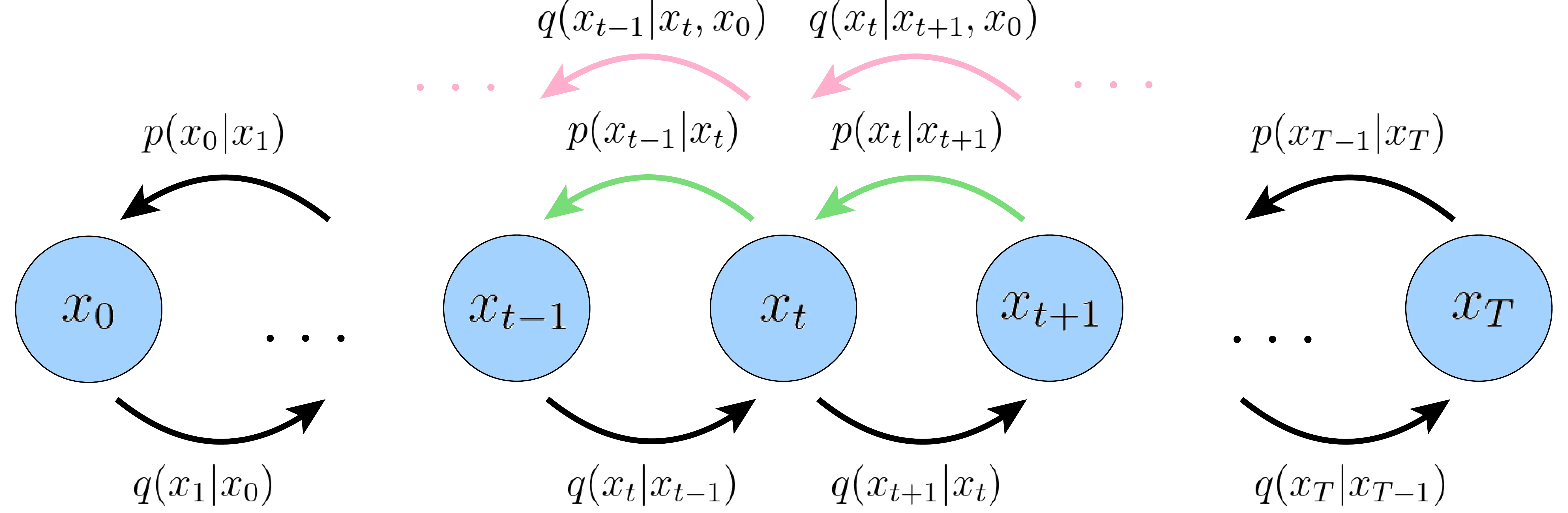
Each denoising term of the variational lower bound compares the KL divergence of the forward process posterior (pink arrow; dependence on original data not shown) and reverse denoising transition (corresponding green arrow); to maximize the VLB, we want to make these distributions as similar as possible. Image from Understanding Diffusion Models: A Unified Perspective.

Denoising Diffusion Probabilistic Models

In this section we will focus on deriving a simple expression for the negative ELBO or variational lower bound (VLB), which in a slight abuse of notation we will call $L_{VLB} = L_0 + L_1 + \ldots + L_{T - 1} + L_T$. Each term is the negative of the corresponding term in the previous section, e.g. $$L_0 = -\mathbb{E}_{q_\phi(x_1 \mid x_0)}[\log{p_\theta(x_0 \mid x_1)}]$$. The particular simplifying assumptions we make along the way give rise to the DDPM model.

Simplifying the ELBO

We will make two further assumptions to simplify this ELBO:

Diffusion Model Encoder Assumption. The latent encoders $q_\phi(x_t \mid x_{t-1})$ are fixed and linear Gaussian; that is, each encoding step is a Gaussian centered on the output of the previous encoding step: $\begin{equation} \label{eq:diff_encoder_assumption} q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{\alpha_t}x_{t-1}, (1 - \alpha_t)I) \end{equation}$ where the noise parameters ${\alpha_t}$ are fixed.

Alternatively, we could parameterize the approximate posterior in terms of a variance schedule $\{\beta_t\}$ as $q(x_t \mid x_{t - 1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t}x_0, \beta_tI)$, with $\alpha_t = 1 -\beta_t$. We will stick to using only using $\alpha_t$s in our following derivation, but in papers it is common to see a mix of $\alpha_t$s and $\beta_t$s.

This means we no longer have to learn the parameters $\phi$ for the encoders, which makes our learning task (and math) easier, and we will drop the $\phi$ subscripts from now on. Furthermore, since the variances are fixed to constants, the prior matching term $L_T = D_{KL}(q(x_T \mid x_0) \vert\vert p(x_T))$ has no learnable parameters and can be ignored during training.

The DDPM probabilistic graphical model. (Figure 2 from the the DDPM paper).

Diffusion Model Prior Assumption. The latent encoder variances $\{\alpha_t\}$ vary such that the distribution $p(x_T)$ of the final latent variable $x_T$ is a standard Gaussian $\mathcal{N}(0, I)$.

This choice makes the prior matching term $L_T$ approximately 0, as long as $q(x_T \mid x_0) \approx \mathcal{N}(0, I)$ (that is, the last latent $x_T$ is totally noisy).

Now we can interpret what the forward and reverse diffusion processes do. In the forward diffusion process, we start from the original data $x_0$ and gradually add noise until it becomes pure Gaussian noise at time $t = T$. In the reverse diffusion process, we start from pure Gaussian noise $x_T \sim \mathcal{N}(0, I)$ and perform a series of denoising steps $p_\theta(x_{t - 1} \mid x_t)$ until we (approximately) recover the original data $x_0$.The dimension, encoder, and prior assumptions are what differentiate a diffusion model from a general MHVAE.

Using the prior assumption, the prior matching term vanishes, so we can write our simpler ELBO as

$\begin{equation} \label{eq:vdm_elbo2_simp} \begin{split} \log{p(x)} \geq & \mathbb{E}_{q(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] \\ & - \sum_{t=2}^{T}{\mathbb{E}_{q(x_{t}| x_0)}[D_{KL}(q(x_{t-1} | x_t, x_0) || p_\theta(x_{t-1} | x_t))]} \end{split} \end{equation}$ By Bayes’ rule, we can invert our key insight $(\ref{eq:vdm_elbo2_key})$:

$\begin{equation} \label{eq:vdm_elbo2_key_inv} q(x_{t-1} | x_t, x_0) = \frac{q(x_t | x_{t-1}, x_0)q(x_{t-1} | x_0)}{q(x_t | x_0)} = \frac{q(x_t | x_{t-1})q(x_{t-1} | x_0)}{q(x_t | x_0)} \end{equation}$ where the second equality holds due to the Markov property. Since we already know $q(x_t \mid x_{t-1})$ by the encoder assumption $(\ref{eq:diff_encoder_assumption})$, we only need to figure out $q(x_t \mid x_0)$.

Using the reparameterization trick for Gaussian distributions, we can write $q(x_t \mid x_{t-1})$ as

$\begin{equation} \label{eq:reparam_trick} q(x_{t} | x_{t-1}) = \sqrt{\alpha_t}x_{t-1} + \sqrt{1 - \alpha_t}\epsilon_{t-1} \end{equation}$ where $\epsilon_{t-1}$ is a standard Gaussian. Rewriting $x_{t-1}$ with the reparameterization trick as well results in:

$\begin{equation} \label{eq:reparam_ind1} \begin{split} x_t & = \sqrt{\alpha_t}x_{t-1} + \sqrt{1 - \alpha_t}\epsilon_{t-1} \\ & = \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1 - \alpha_{t-1}}\epsilon_{t-2}) + \sqrt{1 - \alpha_t}\epsilon_{t-1} \\ & = \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + \sqrt{\alpha_t(1 - \alpha_{t-1})}\epsilon_{t-2} + \sqrt{1 - \alpha_t}\epsilon_{t-1} \\ \end{split} \end{equation}$ Since the sum of two independent Gaussian random variables is again a Gaussian random variable whose mean is the sum of the means and whose variance is the sum of the variances See e.g. https://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables., we can simplify this to

$\begin{equation} \label{eq:reparam_ind2} \begin{split} x_t & = \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + \sqrt{\alpha_t(1 - \alpha_{t-1})}\epsilon_{t-2} + \sqrt{1 - \alpha_t}\epsilon_{t-1} \\ & = \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + \sqrt{(\sqrt{\alpha_t(1 - \alpha_{t-1})})^2 + (\sqrt{1 - \alpha_t})^2}\epsilon_{t-2} \\ & = \sqrt{\alpha_t\alpha_{t-1}}x_{t-2} + \sqrt{1 - \alpha_t\alpha_{t-1}}\epsilon_{t-2} \\ & = \ldots \\ & = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon_0 \end{split} \end{equation}$ where $\bar{\alpha}_t = \prod_{i = 1}^{t}{\alpha_i}$.

Since we have a closed form expression for the forward sampling process $q(x_t \mid x_0)$ in terms of the original data $x_0$, which we know, this means that we don’t have to run the diffusion process forward one step at a time; instead, we can directly sample $x_t$ from $q(x_t \mid x_0) \sim \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I)$.

The Denoising Terms $L_{1:T - 1}$

Continuing our derivation for ground truth posterior $q(x_{t-1} \mid x_t, x_0)$ we can then plug this into $(\ref{eq:vdm_elbo2_key_inv})$ to get

$\begin{equation} \begin{split} q(x_{t-1} | x_t, x_0) & = \frac{q(x_t | x_{t-1})q(x_{t-1} | x_0)}{q(x_t | x_0)} \\ & = \frac{\mathcal{N}(x_t; \sqrt{\alpha_t}, (1 - \alpha_t)I)\mathcal{N}(x_{t-1}; \sqrt{\bar{\alpha}_{t-1}}, (1 - \bar{\alpha}_{t-1})I)}{\mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}, (1 - \bar{\alpha}_t)I)} \\ & \propto \mathcal{N}(x_{t-1}; \frac{\sqrt{\alpha_{t}}(1 - \bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1 - \bar{\alpha}_t}, \frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}) \end{split} \end{equation}$ Define

\[\begin{equation} \label{eq:denoising_mean} \mu_q(x_t, x_0) = \frac{\sqrt{\alpha_{t}}(1 - \bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1 - \bar{\alpha}_t} \end{equation}\]

$\begin{equation} \label{eq:denoising_var} \sigma_q^2(t) = \frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \end{equation}$ Since we know that our ground truth denoising transition $q(x_{t-1} \mid x_t, x_0)$ is a Gaussian with fixed covariance $\sigma_q^2(t)I$ (which only depends on the fixed $\{\alpha_t\}$), we can model our denoising step $p_\theta(x_{t-1} \mid x_t)$ as the following:

$\begin{equation} \label{eq:denoising_trans_dist} p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_q^2(t)I) \end{equation}$ where $\mu_\theta(x_t, t)$ is a function approximator (e.g. a neural network) of the denoising mean, parameterized by $\theta$.

The KL divergence of two multivariate Gaussians $\mathcal{N}_0 = \mathcal{N}(\mu_0, \Sigma_0)$ and $\mathcal{N}_1 = \mathcal{N}(\mu_1, \Sigma_1)$ can be expressed in closed form as

$\begin{equation} \label{eq:mult_norm_kl_div} D_{KL}(\mathcal{N}_0 || \mathcal{N}_1) = \frac{1}{2}(\mbox{tr}(\Sigma_1^{-1}\Sigma_0) + (\mu_1 - \mu_0)^{T}\Sigma_1^{-1}(\mu_1 - \mu_0) + \ln\frac{\det{\Sigma_1}}{\det{\Sigma_0}}) \end{equation}$ Using the fact that the covariances are equal, we see that the expression collapses into something that looks like a reconstruction loss:

$\begin{equation} \label{eq:kl_div_denoise} D_{KL}(q(x_{t-1} | x_t, x_0) || p_\theta(x_{t-1} | x_t)) = \frac{1}{2\sigma_q^2}||\mu_\theta - \mu_q(x_t, x_0)||_2^2 \end{equation}$ We can further simplify our function approximator $\mu_\theta(x_t, t)$ by parameterizing it to match the form of our ground truth mean given by $(\ref{eq:denoising_mean})$:

$\begin{equation} \label{denoising_mean_fn_approx} \mu_\theta(x_t, t) = \frac{\sqrt{\alpha_{t}}(1 - \bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)\hat{x}_\theta(x_t, t)}{1 - \bar{\alpha}_t} \end{equation}$ where $\hat{x}_\theta(x_t, t)$ tries to predict the original data $x_0$ from a noisified version $x_t$ and a time index $t$. We can then express the denoising matching loss $L_{1:T-1}$ as

$\begin{equation} \label{eq:loss_data_recon_weighted} \begin{split} L_{1:T - 1} & = \sum_{t=2}^{T}{\mathbb{E}_{q(x_t | x_0)}[D_{KL}(q(x_{t-1} | x_t, x_0) || p_\theta(x_{t-1} | x_t))]} \\ & = \sum_{t = 2}^{T}{\mathbb{E}_{q(x_t | x_0)}[\frac{1}{2\sigma_q^2}\frac{\bar{\alpha}_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2}||\hat{x}_\theta(x_t, t) - x_0||_2^2]} \end{split} \end{equation}$ Our optimization problem for the denoising terms then becomes

\[\begin{equation} \label{eq:loss_source_denoise_opt} \begin{split} & \quad \underset{\theta}{\arg\min}\, \sum_{t = 2}^{T}{\mathbb{E}_{q(x_t | x_0)}[\frac{1}{2\sigma_q^2}\frac{\bar{\alpha}_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2}||\hat{x}_\theta(x_t, t) - x_0||_2^2]} \\ & = \underset{\theta}{\arg\min}\, \mathbb{E}_{t \sim U\{2, T\}}[\mathbb{E}_{q(x_t | x_0)}[\frac{1}{2\sigma_q^2}\frac{\bar{\alpha}_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2}||\hat{x}_\theta(x_t, t) - x_0||_2^2]] \\ \end{split} \end{equation}\]

We can approximate the expectations with samples: first, we sample random noise levels $t$, and then we randomly sample $x_t \sim q(x_t \mid x_0)$, whose distribution is fixed and can be calculated in closed form by $(\ref{eq:reparam_ind2})$. Finally, we can use the sampled $x_t$ and $t$ to calculate a Monte Carlo estimate of the loss via $\vert\vert\hat{x}_\theta(x_t, t) - x_0\vert\vert_2^2$.

Learning Noise Instead of Signal

Recall that by equation $(\ref{eq:reparam_ind2})$, we have

\[x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon_0\]

where $x_0$ is the original data and $\epsilon_0 \sim \mathcal{N}(\epsilon; 0, I)$ is the “source noise”. We can rearrange this in terms of $x_0$ to get

\[\begin{equation} \label{eq:reparam_ind_noise} x_0 = \frac{x_t - \sqrt{1 - \bar{\alpha}}\epsilon_0}{\sqrt{\bar{\alpha}_t}} \end{equation}\]

We can use this expression to reparameterize our ground truth denoising mean $\mu_q(x_t, x_0)$ as a function of $x_t$ and $\epsilon_0$:

\[\begin{equation} \label{eq:denoising_mean_noise} \begin{split} \mu_q(x_t, \epsilon_0) & = \frac{\sqrt{\alpha_{t}}(1 - \bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}(1-\alpha_t)}x_0}{1 - \bar{\alpha}_t} \\ & = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1 - \alpha_t}{\sqrt{(1 - \bar{\alpha}_t)(\alpha_t)}}\epsilon_0 \end{split} \end{equation}\]

Analogously, we can set our function approximation $\mu_\theta(x_t, t)$ to have the form

\[\begin{equation} \label{eq:denoising_mean_noise_fn_approx} \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1 - \alpha_t}{\sqrt{(1 - \bar{\alpha}_t)(\alpha_t)}}\hat{\epsilon}_\theta(x_t, t) \end{equation}\]

So we can rewrite out denoising matching loss $L_{1:T - 1}$ as

$\begin{equation} \label{eq:loss_noise_recon} L_{1:T - 1} = \mathbb{E}_{t \sim U\{2, T\}}[\frac{1}{2\sigma_q^2}\frac{(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)\alpha_t}\mathbb{E}_{q(x_t | x_0)}[||\hat{\epsilon}_\theta(x_t, t) - \epsilon_0||_2^2]] \end{equation}$ where we learn to predict the source noise $\epsilon_0$ using our function approximator $\hat{\epsilon}_\theta(x_t, t)$.

Although learning a model $\hat{x}_\theta(x_t, t)$ to reconstruct the original data $x_0$ and learning a model $\hat{\epsilon}_\theta(x_t, t)$ to reconstruct the source noise $\epsilon_0$ are mathematically equivalent, the DDPM paper found that modeling the source noise achieves better performance empirically. (More details are in the next section).

The Reconstruction Term $L_0$

As a bit of a recap, our goal is to simplify the negative variational lower bound (VLB) $L_{VLB} = L_0 + L_1 + \ldots + L_{T - 1} + L_T$ into an expression we can implement. By the diffusion encoder assumption $(\ref{eq:diff_encoder_assumption})$, we know that the prior matching term $L_T$ is 0, and the denoising matching terms $L_{1:T - 1}$ are given by $(\ref{eq:loss_data_recon_weighted})$ (if we are modeling the original data $x_0$) or $(\ref{eq:loss_noise_recon})$ (if we are modeling the source noise $\epsilon_0$).

This leaves us with the reconstruction term $L_0 = -\mathbb{E}_{x_1 \sim q(x_1 \mid x_0)}[\log{p_\theta(x_0 \mid x_1)}]$ as the final term we haven’t dealt with. Our denoising model suggests that the distribution $p_\theta(x_0 \mid x_1)$ of the data $x_0$ given $x_1$ should be $\mathcal{N}(x_0; \mu_\theta(x_1, 1), \sigma_1^2)$ (and this is how we modeled $L_1, \ldots, L_{T - 1}$).

However, in the case of images, each dimension of the image is an integer in $\{0, 1, \ldots, 255\}$ and we typically scale the data linearly into $[-1, 1]$ before feeding it into our model. So to obtain a discrete (negative) log likelihood for image data, the DDPM authors choose to use an independent discrete decoder based on $\mathcal{N}(x_0; \mu_\theta(x_1, 1), \sigma_1^2)$. That is, we model $p_\theta(x_0 \mid x_1)$ as

$\begin{equation} \label{eq:ddpm_recon_decoder} p_\theta(x_0 | x_1) = \prod_{i = 1}^{D}{\int_{\delta_{-}(x_0^i)}^{\delta_{+}(x_0^i)}{\mathcal{N}(x_0; \mu_\theta^i(x_1, 1), \sigma_1^2)dx}} \end{equation}$ where

\[\begin{equation*} \delta_{-}(x) = \begin{cases} -\infty & \text{if } x = -1 \\ x - \frac{1}{255} & \text{if } x > -1 \\ \end{cases} \end{equation*}\] \[\begin{equation*} \delta_{+}(x) = \begin{cases} x + \frac{1}{255} & \text{if } x < 1 \\ \infty & \text{if } x = 1 \\ \end{cases} \end{equation*}\]

and $x^i$ refers to the $i$th coordinate of $x$. We could then calculate the (negative) log likelihood of the data under this distribution and then backpropagate through the resulting expression.

It turns out that we don’t need to worry about the decoder, since the DDPM authors found that using the following simplified variant of the variational lower bound leads to better sample quality:

\[\begin{equation} \label{eq:ddpm_obj_simp} L_{\mbox{simple}}(\theta) = \mathbb{E}_{t \sim U[1, t]}[\mathbb{E}_{\epsilon_0 \sim \mathcal{N}(0, I)}[||\hat{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon_0, t) - \epsilon_0||_2^2]] \end{equation}\]

In this objective, the $t = 1$ case corresponds to the reconstruction loss term in the ELBO. For the $t > 1$ terms, this can be viewed as an weighted version of the original variational lower bound $(\ref{eq:loss_noise_recon})$. Relative to $L_{VLB}$, we increase the relative weight of the terms with higher noise levels $t$, which are more difficult to learn, which the DDPM authors say account for its improved performance. As usual, we can optimize this objective using Monte Carlo samples.

In the DDPM paper, the authors found that modeling the original data and modeling the source noise using the original loss functions performed about equally well, but modeling the source noise with the simplified objective $(\ref{eq:ddpm_obj_simp})$ results in a noticeable improvement in generation quality. Interestingly, dropping the time-dependent coefficients from the $L_t$ terms doesn’t seem to work when modeling the original data.

Summary of DDPM Math

A variational diffusion model can be thought of as a Markovian hierarchical variational autoencoder (MHVAE) with the following restrictions:

Diffusion Model Latent Dimension Assumption: the dimension of the latent variables $z_{1:T}$ equals the dimension of the data variable $x$. This allows us to consider the latent variables as representing “noisified” versions $x_{1:T}$ of the original data $x_0$.
Diffusion Model Encoder Assumption: The forward encoders $q_\phi(x_t \mid x_{t-1})$ are fixed, not learned, and are modeled as a Gaussian centered on the output of the previous encoding step: $q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{\alpha_t}x_{t-1}, (1 - \alpha_t)I)$. We can think of the noise parameters $\{\alpha_t\}$ as being hyperparameters of the model; it is possible to extend the model to learn them.
Diffusion Model Prior Assumption: The noise parameters $\{\alpha_t\}$ vary such that the distribution $p(x_T)$ of the final latent variable $x_T$ is a standard Gaussian. That is, at the end of the forward diffusion process, the data is “totally random”.

With these assumptions, we can derive a variational lower bound of the form $\log{p(x)} \geq L_0 + L_1 + \ldots L_{t - 1} + \ldots + L_T$ where

$\begin{equation} \label{eq:summary_diff_vlb} \begin{split} L_0 & = \mathbb{E}_{x_1 \sim q(x_1 | x_0)}[\log{p_\theta(x_0 | x_1)}] \\ L_{t - 1} & = -\mathbb{E}_{x_t \sim q(x_t | x_0)}[D_{KL}(q(x_{t - 1} | x_t, x_0) || p_\theta(x_{t - 1} | x_t))] \\ L_T & = -D_{KL}(q(x_T | x_0) || p(x_T)) \\ \end{split} \end{equation}$ Furthermore, we know that the prior matching term $L_T$ has no learnable parameters via the encoder assumption.

Crucially, we can express the data $x_t$ at noise level $t$ in closed form as a function of the original data $x_0$:

\[\begin{equation} \label{eq:summary_forward_process_posterior} x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon_0 \end{equation}\]

where $\bar{\alpha}_t = \prod_{i=1}^{t}{\alpha_i}$ and $\epsilon_0 \sim \mathcal{N}(0, I)$ is a noise variable. (By the reparameterization trick, this is equivalent to saying that $q(x_t \mid x_0) \sim \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I)$.)

From this and the construction of the encoders in the encoder assumption above, we find that the ground truth denoising transition or forward process posterior $q(x_{t-1} \mid x_t, x_0)$ is also a Gaussian $q(x_{t-1} \mid x_t, x_0) \sim \mathcal{N}(x_{t-1}; \mu_q(x_t, x_0), \sigma_q^2(t)I)$ where

\[\begin{equation} \label{eq:summary_reverse_ground_truth_posterior_signal} \begin{split} \mu_q(x_t, x_0) & = \frac{\sqrt{\alpha_{t}}(1 - \bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1 - \bar{\alpha}_t} \\ \sigma_q^2(t) & = \frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \\ \end{split} \end{equation}\]

This suggests that we should model our learned denoising transition $p_\theta(x_{t-1} \mid x_t)$ as a Gaussian $\mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_\theta^2(x_t, t)I)$ as well. There are several choices of parameterization we can use for our Gaussian distribution. Since our forward posterior variance $\sigma_q^2(t)$ depends only on $t$, a natural choice is to set the variance $\sigma_\theta^2(x_t, t)$ of our denoising transition to be fixed and equal to $\sigma_q^2(t)$.

For the denoising mean $\mu_\theta(x_t, t)$, one choice of parameterization we can make is to set

\[\begin{equation} \label{eq:summary_orig_data_mean_param} \mu_\theta(x_t, t) = \frac{\sqrt{\alpha_{t}}(1 - \bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)\hat{x}_\theta(x_t, t)}{1 - \bar{\alpha}_t} \end{equation}\]

where $\hat{x}_\theta(x_t, t)$ is a model which learns to reconstruct the original data $x_0$ from a noisified version $x_t$ and the time index $t$. Plugging this into our ELBO, we get a denoising objective $L_{1:T - 1}$ of the form

\[\begin{equation} \label{eq:summary_orig_data_denoising_obj} L_{1:T - 1}(\theta) =\mathbb{E}_{x_t, t}[\frac{1}{2\sigma_q^2(t)}\frac{\bar{\alpha}_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2}||\hat{x}_\theta(x_t, t) - x_0||_2^2] \end{equation}\]

where $x_t \sim q(x_t \mid x_0)$ and $t \sim \mbox{Uniform}[2, T]$.

Alternatively, we can rewrite the ground truth mean in terms of $x_t$ and the source noise $\epsilon_0 \sim \mathcal{N}(0, I)$ using $(\ref{eq:summary_forward_process_posterior})$:

\[\begin{equation} \label{eq:summary_reverse_ground_truth_posterior_noise} \mu_q(x_t, \epsilon_0) = \frac{1}{\sqrt{\alpha}_t}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}}\epsilon_0) \end{equation}\]

This suggests an alternate parameterization

\[\begin{equation} \label{eq:summary_source_noise_mean_param} \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha}_t}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}}\hat{\epsilon}_\theta(x_t, t)) \end{equation}\]

where $\hat{\epsilon}_\theta(x_t, t)$ is a model that learns to reconstruct the source noise $\epsilon_0$ from a noisified version of the data $x_t$ and the time index $t$. This yields a denoising objective of the form

\[\begin{equation} \label{eq:summary_source_noise_denoising_obj} L_{1:T - 1}(\theta) = \mathbb{E}_{x_t, t, \epsilon_0}[\frac{1}{2\sigma_q^2(t)}\frac{(1 - \alpha_t)^2}{\alpha_t(1 - \bar{\alpha}_t)}||\hat{\epsilon}_\theta(x_t, t) - \epsilon_0||_2^2] \end{equation}\]

where $x_t \sim q(x_t \mid x_0)$, $t \sim \mbox{Uniform}[2, T]$, and $\epsilon_0 \sim \mathcal{N}(0, I)$.

We could model the log likelihood term $L_0(\theta) = \mathbb{E}_{q(x_1 \mid x_0)}[\log{p_\theta(x_0 \mid x_1)}]$ with an explicit decoder, but instead it is common to drop the time-dependent coefficients and use the simplified objective

\[\begin{equation} \label{eq:summary_simp_denoising_obj} L_{\mbox{simple}}(\theta) = \mathbb{E}_{t, x_0, \epsilon_0}[||\hat{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon_0, t) - \epsilon_0||_2^2] \end{equation}\]

where $t \sim \mbox{Uniform}[1, T]$ and $\epsilon_0 \sim \mathcal{N}(0, I)$. The $t = 1$ case approximates the log likelihood term $L_0$ in the variational lower bound.

For training, we can optimize $(\ref{eq:summary_simp_denoising_obj})$ by approximating the expectation with samples and using a gradient-based optimizer such as Adam. For sampling, we can run the reverse diffusion process one step at a time, repeatedly applying denoising transitions $p_\theta(x_{t - 1} \mid x_t)$ (using the parameterization we chose in $(\ref{eq:summary_source_noise_mean_param})$) until we get to the final denoising mean $\mu_\theta(x_1, 1)$, which we output as our sample.

Implementing a DDPM Model

We need the following ingredients to implement a DDPM-style diffusion model:

A model $\hat{x}_\theta(x_t, t)$ to model the original data or a model $\hat{\epsilon}_\theta(x_t, t)$ to model the source noise. Our model needs a way to encode the time index $t$ as part of its input.
A variance schedule to set the variance parameters $\{\beta_t\} = \{1 - \alpha_t\}$. We want the variances to be monotonically increasing throughout the diffusion process, e.g. $0 < \beta_1 < \beta_2 < \ldots < \beta_T < 1$.
The loss function, which takes samples an arbitrary time index $t$ and then samples from $q(x_t \mid x_0)$ and calculates the appropriate loss, as described below.

Following the DDPM paper, we will choose to model the source noise $\hat{\epsilon}_\theta(x_t, t)$ and use the simplified loss function $L_{\mbox{simple}}(\theta)$, which were the choices in their best-performing model.

Model Architecture

The most popular model architecture for the reverse process model is a U-Net architecture , which consists of the following parts:

Downsampling Blocks: The downsampling portion of the network consists of blocks which downsamples the image width and height and increases the number of channels. Typically, each block contains some number of residual blocks, followed by a downsample operation.
Bottleneck: The bottleneck portion of the model performs computation on the input at the lowest image resolution (and highest number of feature channels), which occurs in the middle of the model. This computation typically does not change the shape of the incoming tensor.
Upsampling Blocks: The upsampling portion of the model is essentially a mirror image of the downsampling portion: each upsampling block upsamples the image width and height and decreases the number of channels. Like the downsample blocks, each upsample block contains a number of residual blocks, followed by an upsample operation. Additionally, each upsampling block has a residual connection to the output of the corresponding downsampling block at the same resolution.

The overall U-Net structure then consists of $N$ downsample blocks, followed by the bottleneck layer, followed by $N$ corresponding upsample blocks. Since the upsampling layers reverse the effect of the downsampling layers, we get an output of the same resolution shape as the input, so we can imagine a U-Net as a kind of autoencoder.

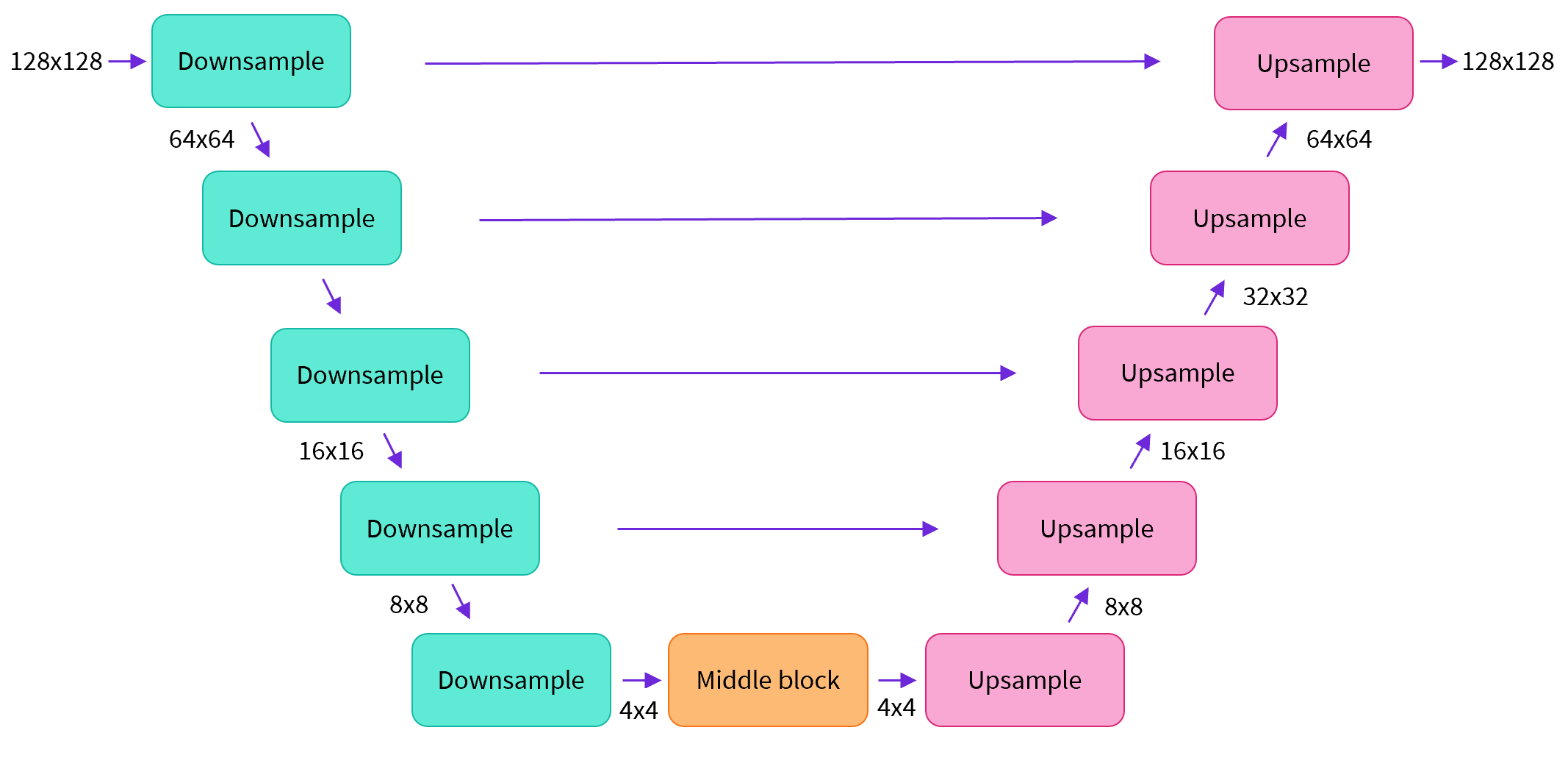
Example U-Net architecture for a 128x128 input image. Image from the diffusers training example notebook.

Additionally, it is common to use an initial and final convolutional layer which do not change the resolution of the representation before the downsampling layers and after the upsampling layers, respectively.

The DDPM U-Net Architecture

In this section, we will discuss the original DDPM U-Net the authors used for the CIFAR10 dataset, accompanied by a sample implementation in PyTorch. This implementation is based on the original Tensorflow implementation and Phil Wang’s PyTorch implementation .

Residual Block

The U-Net in the DDPM paper follows the PixelCNN++ paper by using multiple Wide ResNet-style residual blocks in each downsampling and upsampling block. The original Wide ResNet paper used batch normalization and ReLU activations before each convolution, but the DDPM authors instead opt for group normalization and SiLU activations.

class PreNorm(nn.Module):
    """Applies an activation and then group norm before a submodel fn."""
    def __init__(self, dim, fn, act_fn=nn.Identity(), groups=1) -> None:
        super().__init__()
        self.fn = fn
        self.act_fn = act_fn
        self.norm = nn.GroupNorm(groups, dim)
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        x = self.norm(x)
        x = self.act_fn(x)
        return self.fn(x)


class ResnetBlock(nn.Module):
    def __init__(self, dim, dim_out, *, time_emb_dim=None, groups=8, dropout=0.1) -> None:
        super().__init__()

        self.act_fn = nn.SiLU()
        self.dropout = nn.Dropout(p=dropout)

        self.conv1 = PreNorm(dim, nn.Conv2d(dim, dim_out, 3, padding=1), self.act_fn, groups=groups)
        self.conv2 = PreNorm(dim_out, nn.Conv2d(dim_out, dim_out, 3, padding=1), self.act_fn, groups=groups)
        self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()

        # For the time embedding
        self.mlp = (
            nn.Sequential(nn.SiLU(), nn.Linear(time_emb_dim, dim_out))
            if exists(time_emb_dim)
            else None
        )
    
    def forward(self, x, time_emb=None):
        h = self.conv1(x)

        # Add the time step embedding, if available.
        if exists(self.mlp) and exists(time_emb):
            time_emb = self.mlp(time_emb)
            time_emb = rearrange(time_emb, "b c -> b c 1 1")
            h += time_emb
        
        h = self.dropout(h)
        h = self.conv2(h)

        return h + self.res_conv(x)

Additionally, the DDPM authors introduce the usage of multi-head attention at the 16x16 resolution, for both downsampling and upsampling. The dot-product attention operation on queries $Q$ and keys $K$ of dimension $d_k$, and values $V$ is :

\[\begin{equation} \label{dot_prod_attn} \mbox{Attention}(Q, K, V) = \mbox{softmax}(\frac{QK^T}{\sqrt{d_k}})V \end{equation}\]

In our case, the input into our attention block is an intermediate U-Net representation (in NCHW format), which we project into different subspaces using a convolutional layer.

class Attention(nn.Module):
    """Standard multi-head attention as in a Transformer. We allow all tokens
    to attend to each other, unlike a standard Transformer in NLP."""
    def __init__(self, dim: int, heads: int=4, dim_head: int=32) -> None:
        super().__init__()
        self.scale = dim_head ** -0.5
        self.heads = heads
        hidden_dim = dim_head * heads
        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
        self.to_out = nn.Conv2d(hidden_dim, dim, 1)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        b, c, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, dim=1)
        q, k, v = map(
            lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads),
            qkv
        )
        q = q * self.scale

        sim = torch.einsum("b h d i, b h d j -> b h i j", q, k)
        sim = sim - sim.amax(dim=-1, keepdim=True).detach()
        attn = sim.softmax(dim=-1)

        out = torch.einsum("b h i j, b h d j -> b h i d", attn, v)
        out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
        return self.to_out(out)

Because the original dot-product attention operation is computationally expensive, we opt to use a linear self-attention variant from in downsampling/upsampling layers.

Time Embedding

Since our model $\epsilon_\theta(x_t, t)$ depends on the time index $t$, we need some way to incorporate this information into our model. The DDPM authors accomplish this by using a sinusoidal position embedding very similar to the one used in the Transformer model to encode $t$, and then add the embeddings to each residual block in both the down and upsampling layers.

class SinusoidalPositionEmbeddings(nn.Module):
    def __init__(self, dim: int):
        super().__init__()
        self.dim = dim
    
    def forward(self, time: torch.Tensor) -> torch.Tensor:
        # Assume time is a tensor with shape (batch_size, 1)
        device = time.device
        half_dim = self.dim // 2
        embeddings = math.log(10000) / (half_dim - 1)
        embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
        embeddings = time[:, None] * embeddings[None, :]
        embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
        return embeddings

Downsample Layers

Each downsample layer of the U-Net then consists of a number of residual blocks, followed by a downsample operation which reduces the spatial dimensions of the representation by 2x:

def Downsample(dim: int, dim_out: Optional[int]=None) -> nn.Module:
    return nn.Sequential(
        Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),
        nn.Conv2d(dim * 4, default(dim_out, dim), 1),
    )

This isn’t exactly the same as the downsample operation used by the original DDPM implementation, but is very similar in that it consists of a convolutional layer which downsamples the resolution by 2x.

In addition, each downsample layer also increases the number of channels in the representation by a fixed multiple. The DDPM authors had each downsample layer after the first increase the number of channels by 2x, so that relative to the number of input channels, the number of channels in the downsample representations increases as powers of 2: 1, 2, 4, 8,… This choice has been adopted by most subsequent diffusion U-Net models.

Upsample Layers

We can think of each upsample layer as “undoing” the effects of the downsample layer at the same spatial resolution: it increases the spatial extent of the representation and decreases the number of channels of the representation by the corresponding amounts. The upsample layers are laid out in the mirror image of the downsample layers.

Each upsample layer consists of the same number of residual blocks as each downsample layer, followed by a upsample operation:

def Upsample(dim: int, dim_out: Optional[int]=None) -> nn.Module:
    return nn.Sequential(
        nn.Upsample(scale_factor=2, mode="nearest"),
        nn.Conv2d(dim, default(dim_out, dim), 3, padding=1),
    )

Furthermore, each upsample layer has shortcut connections to the downsample layer at the same resolution, with each residual block in the upsample layer connected to the output of the mirror-image residual block in the downsample layer.

Bottleneck Layer

For the bottleneck layer of the U-Net, the DDPM authors used a self-attention layer sandwiched by two ResNet blocks, which preserve the spatial dimensions of the representation.

Summary

Putting everything together, we have the following U-Net implementation:

class DDPMUnet(nn.Module):
    def __init__(
        self,
        dim: int,
        init_dim: Optional[int]=None,
        out_dim: Optional[int]=None,
        dim_mults: Tuple[int, ...]=(1, 2, 4, 8),
        attn_resolutions: Tuple[int, ...]=(16,),
        image_size: int=32,
        channels: int=3,
        resnet_block_groups: int=4,
        dropout: float=0.1,
        use_linear_attn: bool=True,
    ) -> None:
        super().__init__()

        # ----Setup----

        self.channels = channels

        init_dim = default(init_dim, dim)

        dims = [init_dim, *map(lambda m: init_dim * m, dim_mults)]
        resolutions = [image_size // (2 ** n) for n in range(len(dim_mults))]
        in_out = list(zip(dims[:-1], dims[1:], resolutions))

        out_dim = default(out_dim, channels)

        attn_cls = Attention
        if use_linear_attn:
            attn_cls = LinearAttention
        
        res_block = partial(ResnetBlock, groups=resnet_block_groups, dropout=dropout)

        # ----Handle time embeddings----
        time_dim = dim * 4
        self.time_mlp = nn.Sequential(
            SinusoidalPositionEmbeddings(dim),
            nn.Linear(dim, time_dim),
            nn.SiLU(),
            nn.Linear(time_dim, time_dim),
        )

        # ----Downsample Layers----

        # Initial convolutional layer
        self.init_conv = nn.Conv2d(self.channels, init_dim, 3, padding=1)

        self.downsample_layers = nn.ModuleList([])
        num_resolutions = len(in_out)

        for idx, (dim_in, dim_out, image_size) in enumerate(in_out):
            is_last = idx >= (num_resolutions - 1)
            use_attn = image_size in attn_resolutions

            # Each downsample block consists of:
            #   - (ResnetBlock + pre-GroupNorm attention block (if using)) x 2
            #   - 2x Downsample operation x 1
            self.downsample_layers.append(
                nn.ModuleList(
                    [
                        res_block(dim_in, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, attn_cls(dim_out))) if use_attn else nn.Identity(),
                        res_block(dim_out, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, attn_cls(dim_out))) if use_attn else nn.Identity(),
                        Downsample(dim_out, dim_out) if not is_last else nn.Identity(),
                    ]
                )
            )

        # ----Bottleneck Layers----
        mid_dim = dims[-1]
        self.mid_block1 = res_block(mid_dim, mid_dim, time_emb_dim=time_dim)
        self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
        self.mid_block2 = res_block(mid_dim, mid_dim, time_emb_dim=time_dim)

        # ----Upsample Layers----

        self.upsample_layers = nn.ModuleList([])

        for idx, (dim_in, dim_out, image_size) in enumerate(reversed(in_out)):
            is_last = idx >= (num_resolutions) - 1
            use_attn = image_size in attn_resolutions

            # Each upsample block consists of:
            #   - (ResnetBlock + pre-GroupNorm attention block (if using)) x 2
            #   - 2x Upsample operation x 1
            self.upsample_layers.append(
                nn.ModuleList(
                    [
                        res_block(dim_out + dim_out, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, attn_cls(dim_out))) if use_attn else nn.Identity(),
                        res_block(dim_out + dim_out, dim_in, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_in, attn_cls(dim_in))) if use_attn else nn.Identity(),
                        Upsample(dim_in, dim_in) if not is_last else nn.Identity()
                    ]
                )
            )
        
        # Final convolutional layer
        self.final_conv = PreNorm(
            dim,
            nn.Conv2d(dim, out_dim, 3, padding=1),
            act_fn=nn.SiLU(),
            groups=resnet_block_groups,
        )

    def forward(self, x: torch.Tensor, time: torch.Tensor) -> torch.Tensor:
        # x should have initial shape (batch_size, num_channels, height, width)
        # t should have initial shape (batch_size, 1)
        x = self.init_conv(x)

        t = self.time_mlp(time)

        # Stack of intermediate downsample x values for shortcut connections
        # between the downsample and upsample layers at the same resolution.
        h = []

        # Downsample
        for block1, attn1, block2, attn2, downsample in self.downsample_layers:
            x = block1(x, t)
            x = attn1(x)
            h.append(x)

            x = block2(x, t)
            x = attn2(x)
            h.append(x)

            x = downsample(x)
        
        # Bottleneck
        x = self.mid_block1(x, t)
        x = self.mid_attn(x)
        x = self.mid_block2(x, t)

        # Upsample
        for block1, attn1, block2, attn2, upsample in self.upsample_layers:
            x = torch.cat((x, h.pop()), dim=1)
            x = block1(x, t)
            x = attn1(x)

            x = torch.cat((x, h.pop()), dim=1)
            x = block2(x, t)
            x = attn2(x)

            x = upsample(x)
        
        # Final conv layer
        x = self.final_conv(x)

        return x

Subsequent work has suggested U-Net architecture improvements for diffusion models, e.g. .

Variance Schedules

In the DDPM paper, the authors used a fixed (as opposed to learned) variance schedule $0 < \beta_1 < \ldots < \beta_T < 1$. The particular hyperparameter settings they used were a linear variance schedule with $\beta_1 = 10^{-4}$ and $\beta_T = 0.02$, with these specific values chosen such that the prior matching term $L_T \approx 0$ and the variances are small relative to the data scaled to $[-1, 1]$.

def cosine_beta_schedule(timesteps, s=0.008):
    steps = timesteps + 1
    x = torch.linspace(0, timesteps, steps)
    alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * torch.pi * 0.5) ** 2
    alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
    betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
    return torch.clip(betas, 0.0001, 0.9999)


def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start, beta_end, timesteps)


def quadratic_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start ** 0.5, beta_end ** 0.5, timesteps) ** 2


def sigmoid_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    betas = torch.linspace(-6, 6, timesteps)
    return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start

In subsequent work, it was found that the choice of a linear variance schedule could be improved on by using a cosine variance schedule. There are also extensions of the model which allow the variances of the reverse diffusion process to be learned jointly with the mean.

Forward Diffusion Process

Since we have a closed-form expression for a noisy image $x_t$ in terms of the original data $x_0$ via $(\ref{eq:summary_forward_process_posterior})$, we do not need to implement the forward diffusion process step-by-step. Instead, we can simply sample directly from $q(x_t \mid x_0) \sim \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I)$, which is often called the forward process posterior:

class DDPM(nn.Module):
	...
	def q_sample(
        self,
        x_start: torch.Tensor,
        t: torch.Tensor,
        noise: Optional[torch.Tensor]=None,
        device: Union[torch.device, str]="cuda" if torch.cuda.is_available() else "cpu",
    ) -> torch.Tensor:
        """Run the forward diffusion process to get x_start at noise level t.
        
        In particular, this samples from q(x_t | x_0) in batch mode via

        \[ x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon_0 \]

        where $\epsilon_0$ is a noise sample sampled from a standard Gaussian.
        """
        if noise is None:
            noise = torch.randn_like(x_start, device=device)
        
        sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)
        sqrt_one_minus_alphas_cumprod_t = extract(
            self.sqrt_one_minus_alphas_cumprod, t, x_start.shape
        )

        return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
	...

Training

We can give the following batch training algorithm for a DDPM model modeling the source noise $\epsilon_0$ using the simplified training objective $(\ref{eq:summary_simp_denoising_obj})$:

Training algorithm for the DDPM model. (Algorithm 1 from the DDPM paper).

Essentially, for each data point $x_0$ we train on, we sample a time step $t \sim \mbox{Uniform}(\{1, \ldots, T\})$ and some source noise $\epsilon \sim \mathcal{N}(0, I)$. We then sample from the forward process posterior $q(x_t \mid x_0) \sim \mathcal{N}(\sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I)$ using the reparameterization trick and take a gradient step on the loss term associated with $t$, which is the reconstruction loss $\vert\vert\epsilon - \hat{\epsilon}_\theta(x_t, t)\vert\vert^2$.

def train_one_epoch(
    epoch: int,
    dataloader: DataLoader,
    model,
    optimizer,
    ema,
    device,
    writer,
    timesteps: int=200,
    loss_type: str="huber",
):
    model.train()
    epoch_loss = 0.0
    progress_bar = tqdm(range(len(dataloader)))
    progress_bar.set_description(f"Epoch {epoch} Steps")
    for step, (batch, _) in enumerate(dataloader):
        batch_size = batch.shape[0]
        batch = batch.to(device)

        # Sample timesteps uniformly at random from [0,..., T - 1] each sample
        # in the batch.
        t = torch.randint(0, timesteps, (batch_size,), device=device).long()

        # The model forward pass occurs in the loss function.
        loss = model.p_losses(batch, t, loss_type=loss_type, device=device)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

        # Update the parameters via EMA, if applicable.
        if exists(ema):
            ema.update()
        
        step_loss = loss.detach().item()
        epoch_loss += step_loss
        
        logs = {"step_loss": step_loss}
        progress_bar.set_postfix(**logs)
        progress_bar.update(1)
    
    epoch_loss /= step
    writer.add_scalar('metrics/training_loss', epoch_loss, epoch)

    return epoch_loss

The DDPM authors use exponential moving averaging (EMA) during training, and then use the EMA-averaged model weights for evaluation. Since there is no native PyTorch support for EMA (as of the time of writing and 1.13.0), we use the torch-ema package; ema-pytorch is another choice.

An implementation of the simplified loss $(\ref{eq:summary_simp_denoising_obj})$ is

class DDPM(nn.Module):
	...
	def p_losses(
        self,
        x_start: torch.Tensor,
        t: torch.Tensor,
        noise: Optional[torch.Tensor]=None,
        loss_type: str="l2",
        device: Union[torch.device, str] = "cuda" if torch.cuda.is_available() else "cpu",
    ) -> torch.Tensor:
        """Implements the simplified loss function from the DDPM paper.
        
        This implements equation (14) from the paper:

        \[L(\theta) = \mathbb{E}_{t, x_0, \epsilon}[||\epsilon - \epsilon_\theta(x_t, t)||_2^2\]

        via a single-sample estimate for a batch of x_t and t.
        """
        if noise is None:
            noise = torch.randn_like(x_start, device=device)
        
        # Get x_t samples from q(x_t | x_0)
        x_noisy = self.q_sample(x_start=x_start, t=t, noise=noise, device=device)

        # Get noise predictions from our denoising model $\epsilon_\theta(x_t, t)$.
        predicted_noise = self.denoise_model(x_noisy, t)

        # L_simple uses the L2 loss, but we implement the ability to experiment
        # with other reconstruction losses.
        if loss_type == 'l1':
            loss = F.l1_loss(noise, predicted_noise)
        elif loss_type == 'l2':
            loss = F.mse_loss(noise, predicted_noise)
        elif loss_type == 'huber':
            loss = F.smooth_l1_loss(noise, predicted_noise)
        else:
            raise NotImplementedError(f"Loss type {loss_type} is not implemented.")
        
        return loss
	...

Sampling

We now know how to train a diffusion model. After training a model, how can we sample from it?

As with other generative models, we start with a noise sample $x_T \sim \mathcal{N}(x_T; 0, I)$ from our prior $p(x_T)$. We then run the reverse diffusion process one step at a time:

class DDPM(nn.Module):
	...
	@torch.no_grad()
	def p_sample_loop(
		self,
		shape,
		device: Union[torch.device, str]="cuda" if torch.cuda.is_available() else "cpu",
	):
		"""Implements the sampling loop for the reverse diffusion process.

		This runs the reverse diffusion process from timestep T - 1 down to 0,
		getting samples at timestep t using the p_sample() method.
		"""
		b = shape[0]
		# Start from pure noise for each sample in the batch.
		img = torch.randn(shape, device=device)
		imgs = []

		for i in tqdm(
			reversed(range(0, self.timesteps)),
			desc='sampling loop time step',
			total=self.timesteps
			):
			img = self.p_sample(
				img,
				torch.full((b,), i, device=device, dtype=torch.long),
				i
			)
			imgs.append(img.cpu())
		
		return imgs

	@torch.no_grad()
	def sample(
		self,
		batch_size: int=16,
		channels: int=3,
		image_size: int=28,
		device: Union[torch.device, str]="cuda" if torch.cuda.is_available() else "cpu",
	):
		"""Sample from the diffusion model by running the reverse diffusion process."""
		return self.p_sample_loop(
			shape=(batch_size, channels, image_size, image_size), device=device
		)
	...

By construction, we know that $p_\theta(x_{t - 1} \mid x_t)$ has distribution $\mathcal{N}(\frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}}\hat{\epsilon}_\theta(x_t, t)), \sigma_q^2(t)I)$ (from $(\ref{eq:summary_source_noise_mean_param})$). Using the reparameterization trick, we can first sample some noise $z \sim \mathcal{N}(0, I)$, and then sample $x_{t - 1}$ according to

\[x_{t - 1} = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}}\hat{\epsilon}_\theta(x_t, t)) + \sigma_q(t)z\]

At the last denoising step, we output the denoising mean $x_0 = \mu_\theta(x_1, 1)$ without any noise.

class DDPM(nn.Module):
	...
	@torch.no_grad()
	def p_sample(
		self,
		x: torch.Tensor,
		t: torch.Tensor,
		t_index: int,
	) -> torch.Tensor:
		"""Run one step of the reverse diffusion process.
		
		This implements one step in the loop in Algorithm 2 of the DDPM paper
		in batch modee. Given the previous sample x_t at noise level t, we
		get a sample x_{t-1} at noise level t - 1 using our formula for the
		denoising transition $p_\theta(x_{t-1} | x_t)$ via the
		reparameterization trick.
		"""
		betas_t = extract(self.betas, t, x.shape)

		sqrt_one_minus_alphas_cumprod_t = extract(
			self.sqrt_one_minus_alphas_cumprod, t, x.shape
		)
		sqrt_recip_alphas_t = extract(self.sqrt_recip_alphas, t, x.shape)

		# Use our noise prediction model to predict the mean
		model_mean = sqrt_recip_alphas_t * (
			x - betas_t * self.denoise_model(x, t) / sqrt_one_minus_alphas_cumprod_t
		)

		if t_index == 0:
			return model_mean
		else:
			posterior_variance_t = extract(self.posterior_variance, t, x.shape)
			noise = torch.randn_like(x)
			return model_mean + torch.sqrt(posterior_variance_t) * noise
	...

This algorithm is summarized in the following algorithm:

Sampling algorithm for the DDPM model. (Algorithm 2 from the the DDPM paper).

Metrics and Evaluation

In this section, we will discuss several metrics used for quantitatively evaluating image generation models (which are not specific to diffusion models), with an emphasis on metrics used in the original DDPM paper. The current standard metric is Fréchet Inception Distance (FID), which corresponds well with human judgments; however, it is not considered a “gold standard” and finding better sample quality metrics is still an open research question.

Likelihood and Bits Per Dimension

A natural metric to use is the likelihood of the model. To make results comparable across different models and datasets, this is typically measured in bits per dimension (BPD). For images, this quantity is sometimes called bits per pixel, where each color channel counts as a “pixel”. The formula for bits per dimension $b(x)$ is as follows:

\[\begin{equation} \label{eq:bits_per_dim} b(x) = -\frac{\log{p(x)}}{D\log{2}} \end{equation}\]

Intuitively, we can calculate the bits per dimension by estimating the negative log likelihood, dividing by the number of dimensions $D$, and then converting to bits (hence to $\log{2}$ factor). Here all logarithms are the natural logarithm.

For a diffusion model, we can upper bound the negative log likelihood with the negative variational lower bound $(\ref{eq:summary_diff_vlb})$.

Bits per dimension is often reported on the test set. It can also be used as a measure of whether a generative model is overfitting; for a well-trained model, we expect the training BPD and test BPD to be very similar.

However, using likelihood or bits/dim as a metric has drawbacks. The likelihood can be dominated by single samples, and is often not indicative of the visual sample quality of the model.

Inception Score

The Inception Score (IS) metric was introduced in . The idea is as follows: suppose we are training on a labeled dataset and have a strong classifier model $p(y \mid x)$ on that datset. If we generate a batch of images $x_{gen}$ from a well-trained generative model, we should expect the following to be true:

The objects in the generated images should be distinctive, so $p(y \mid x_{gen})$ should have low entropy: we expect the distribution to be sharply peaked at the label of the object which we generated an image of.
The model should generate a variety of objects in its images, so the marginal distribution of labels $p(y) = \int{p(y \mid x_{gen}) dx_{gen}}$ should have high entropy.

Thus, for a good generative model $G(x)$, we would expect the distributions $p(y \mid x)$ and $p(y)$ to look very different for $x \sim G(x)$, so the KL divergence between them $D_{KL}(p(y \mid x) \vert\vert p(y))$ should be large. So we define the Inception Score metric as follows:

\[\begin{equation} \label{eq:inception_score} IS = \exp(\mathbb{E}_{x \sim G(x)}[D_{KL}(p(y | x) || p(y))]) \end{equation}\]

We exponentiate the KL divergence to make the scores easier to compare. Better generative models should have higher Inception scores; intuitively, either increasing the sample quality of a generative model or the diversity of its generated images should increase the IS.

The paper introducing IS found that it corresponded well with human judgments. However, a drawback of the IS score is that it never references real images directly . Furthermore, IS does not reward covering the whole distribution of images in the dataset and cannot capture intra-class diversity (e.g. generating different breeds of dogs which are all labeled “dog” in the dataset). A final weakness of IS is that models can achieve a high IS simply by memorizing a small subset of the data.

In practice, the classifier of choice for calculating IS is the Inception V3 model (hence the name). For maximum comparability, it is recommended to use the reference implementation , since differences in implementation and backends can affect the scores. Typically, a sample of 50k generated images is used to compute the IS.

Fréchet Inception Distance

The Fréchet Inception Distance (FID) metric was introduced in to address some shortcomings in the Inception score, particularly the fact that it does not compare generated images to real images.

As with the Inception Score, suppose we are training on a labeled dataset and have a strong classifier $p(y \mid x)$ for that dataset. If we have a batch of real images $x_{real} \sim D$ and a batch of generated images $x_{gen} \sim G(x)$ for a generative model $G(x)$, then the more similar the visual features (the latent representation of the classifier before the softmax layer) computed by the classifier on $x_{gen}$ are to the visual features computed on $x_{real}$, the better we would expect the sample quality to be.

To make the notion of “similar” more precise, suppose $X_{real}$ is a random variable holding the value of the classifier visual feature tensor for the real images $x_{real}$, and $X_{gen}$ is defined similarly. In general, $X_{real}$ and $X_{gen}$ might have a very complicated distribution, but we can approximate this distribution using the first and second moments or cumulants, which are the mean and covariance respectively. In particular, we will assume that $X_{real}$ is distributed according to a multivariate Gaussian with mean $\mu_{real}$ and covariance $C_{real}$, and analogously $X_{gen} \sim \mathcal{N}(\mu_{gen}, C_{gen})$. Then the Fréchet Inception Distance is defined as the Fréchet distance between the two Gaussian distributions:

\[\begin{equation} \label{eq:frechet_inception_distance} d^2(X_{real}, X_{gen}) = ||\mu_{real} - \mu_{gen}||_2^2 + \mbox{tr}(C_{real} + C_{gen} + 2\sqrt{C_{real}C_{gen}}) \end{equation}\]

Unlike the IS, better FID scores are lower scores, because it is a measure of distance between distributions. Like the IS, FID correlates well with human judgments.

The FID is considered the standard metric for evaluating generated sample quality as the time of writing. However, as noted above, it is not considered the “gold standard”, and there is ongoing research into developing better sample quality metrics.

In practice, the FID score uses the Inception V3 model as its classifier. The most common choice for the visual features is the output of the final pooling layer (typically called “pool3”) before the classification layer, although other choices are possible. . The reference implementation is in Tensorflow , and there also exist implementations for PyTorch . The FID scores given by different implementation can vary, so for comparability, it is recommended to use the official reference implementation.

Because the dimension of the Inception V3 pool3 layer is 2048, using at least 2048 samples is required to avoid numerical issues. It is common to use at least 10k samples; for example, on the CIFAR-10 dataset, it is common to report the FID on the training set (50k samples) and test set (10k samples). .

Changelist

2023-02-26: Initial post